Demonstrating Some dm Features
A short video demonstrating just a few of the many things you can do with dm, the command-line counterpart to DirMaster.
A short video demonstrating just a few of the many things you can do with dm, the command-line counterpart to DirMaster.
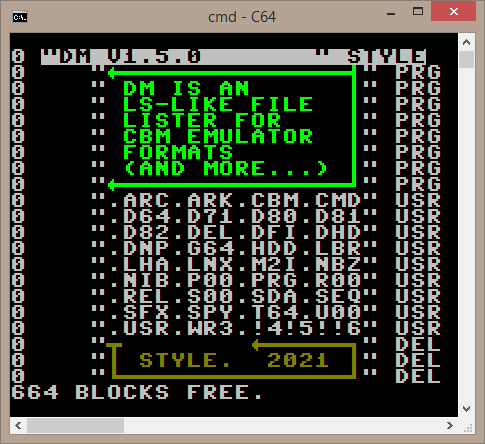
dm is a command line counterpart to DirMaster with a unix-flavored set of features.
dm started out as an ls-like lister for CBM (Commodore Business Machine, i.e. the c64, c128, etc) container formats - that includes both physical-media image formats (like .d64, .t64 .p00) and native/archival formats (like .lnx and [1-4]! zips). dm now includes a growing number of useful sub-commands for performing various tasks on supported container formats that make sense in the command line interface context - think of dm as a CLI 'cousin' to DirMaster. dm was originally called cbmls when its only feature was listing.
Current sub-commands are:
The default when no sub-command is explicitly selected is 'ls' and in that case dm will behave much like cbmls did. But you can also use 'dm ls' if you want to explicitly invoke the ls/listing feature. i.e. the following are equivalent:
dm ls -lc disk.d64
dm -lc disk.d64 # sub-command omitted
See the documentation link above for more information.